拉伸载荷下三维拉胀双层结构的褶皱失稳研究

拉胀材料因其负泊松比特性深度契合生物组织变形，在生物医学领域得到广泛应用。然而，其在应用过程中与生物组织形成的双层结构存在发生褶皱失稳的风险。现有研究主要集中于压缩载荷作用下的褶皱失稳行为，而拉伸所引发的褶皱失稳机理尚不明确，同时，适用于大变形条件下的褶皱失稳理论模型也亟待完善。因此，爱尔兰高威大学Sairam Pamulaparthi Venkata教授团队建立了适用于大变形拉伸载荷条件下的褶皱失稳模型，并进一步分析了泊松比失配对褶皱失稳的影响，为实际应用中抗褶皱提供了新思路。

本文基于Blatz-Ko超弹性本构模型（图1）构建理论框架。首先推导出薄膜与基底的变形梯度和应力关系，进而通过增量分岔理论建立线性失稳条件，并推导高阶渐进表达式用于大变形修正，最后实现半解析求解以预测临界拉伸比λc和波数Kc。通过将理论模型的预测结果与有限元计算结果进行对比，验证了理论模型的有效性和合理性（图2）。

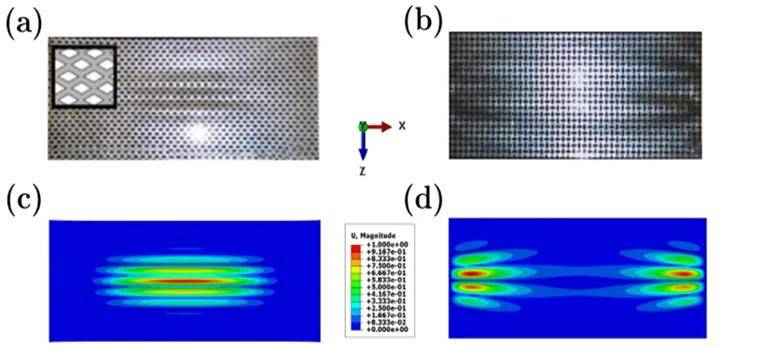
图1 基于Blatz-Ko超弹性本构模型的实验与有限元模拟结果对比

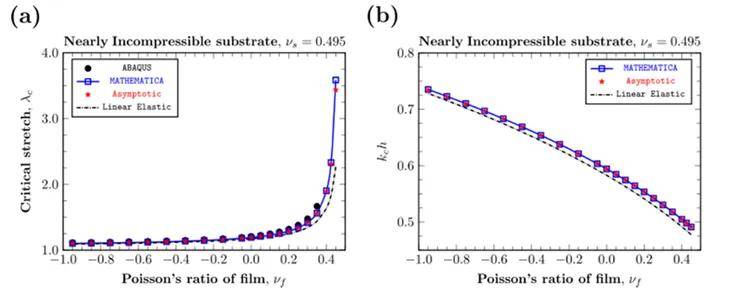
图2 理论解与有限元模拟结果对比

结果表明，当且仅当基底泊松比Vₛ大于薄膜泊松比Vf（Vₛ>Vf）时，才会发生平行于拉伸方向的褶皱失稳现象，这是由于具有更高泊松比的基底发生了更显著的横向收缩，在薄膜内诱发压缩应力（图3）；临界拉伸比λc随| Vₛ - Vf |减小而急剧增大，而皱纹波长则随泊松比差异增大而缩短，但高压缩性材料（Vₛ ≤ -0.7）出现波长反常缩短现象（图4d），表明Blatz-Ko模型对强拉胀行为的预测存在局限。本文进一步结合逆设计方法，成功实现薄膜微结构（正交椭圆/矩形孔）的泊松比靶向调控（图5a），其均质化模型与ABAQUS微结构模拟的临界拉伸比误差<6.3%（图5b）。

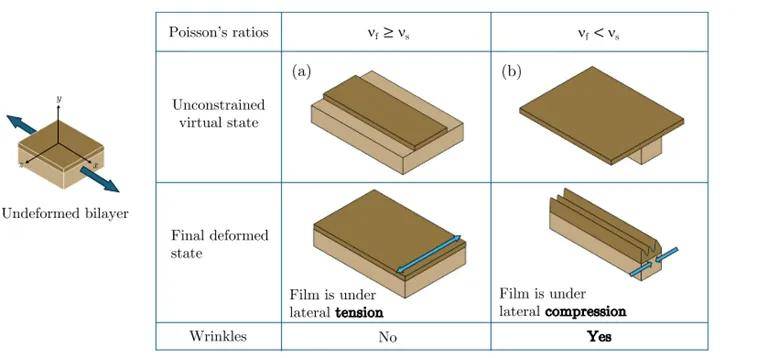
图3 双层结构受拉伸载荷作用示意图

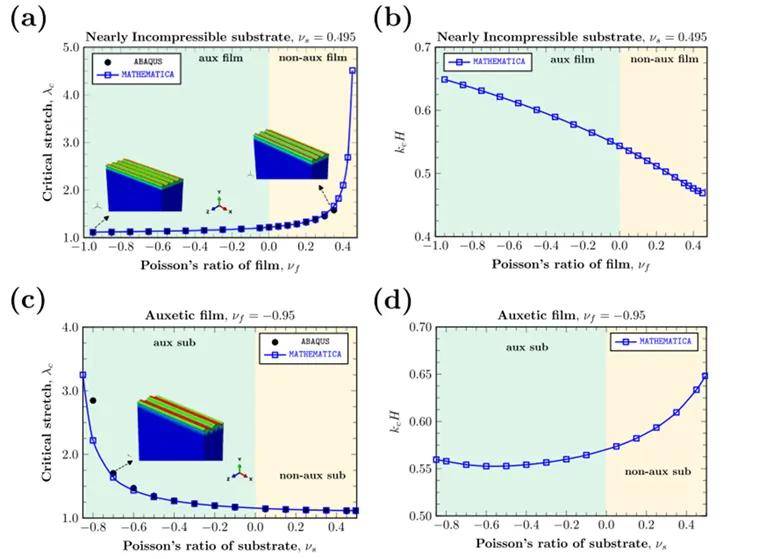
图4 基于Blatz-Ko超弹性模型的有限元模拟结果与理论解对比

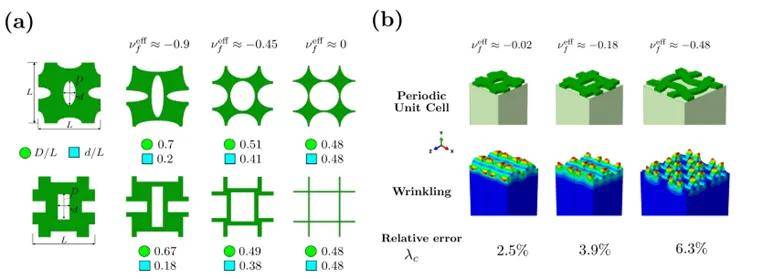
图5 (a)微结构几何形状，(b)不同微结构的双层结构受拉伸载荷褶皱情况

综上所述，本文系统探究了3D拉胀双层结构在单轴拉伸下的起皱不稳定性机制，通过理论建模和数值模拟揭示核心规律。本文通过微结构设计实现褶皱可控，为生物医学器件的抗褶皱设计提供了理论支撑。

相关论文以“Wrinkling instability of 3D auxetic bilayers in tension"为题发表在《Journal of the Mechanics and Physics of Solids》。