一篇文章讲清楚 —— 橡胶的疲劳寿命在研究什么

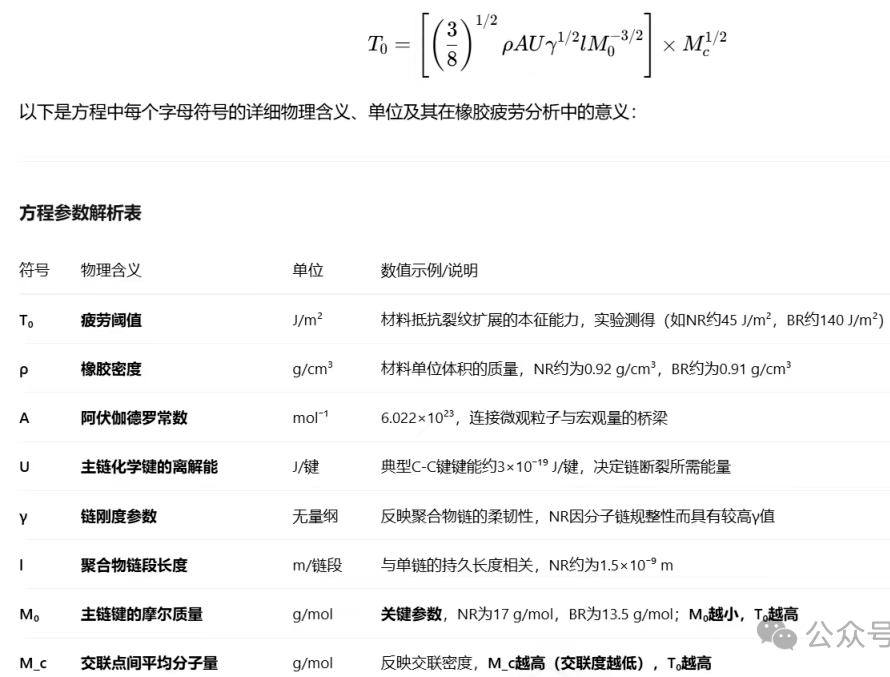
橡胶的疲劳寿命，是指橡胶制品在受到周期性的拉伸、压缩或剪切变形时，抵抗内部或表面产生裂纹并导致其最终断裂的能力，通常用达到破坏时所经历的变形循环次数来表示。

疲劳寿命研究主要分为裂纹形核法和裂纹扩展法两大分支。裂纹形核法关注从微观缺陷到宏观裂纹形成的过程，而裂纹扩展法则聚焦已有裂纹的增长规律。两种方法在理论基础、实验技术和应用场景上各有侧重，共同构成了橡胶疲劳寿命预测的完整体系。

本文将详细分别介绍裂纹形核法与裂纹扩展法，包括以下内容：

1.裂纹形核法

1.1 基本介绍

1.2 应变比对寿命预测的影响

1.3 累计疲劳损伤准则

1.4 随机载荷下的疲劳寿命

2.裂纹扩展法

3.总结

1.裂纹形核法

1.1 基本介绍

裂纹形核法基于微观损伤累积理论，认为疲劳失效是循环载荷下微观缺陷逐步演化的结果。

裂纹形核法的核心机制：分子链断裂，填料脱粘，应力集中效应。

裂纹形核法试件通常长这样，特征是试件上无初始缺陷：

对于橡胶来说，通常考虑获取其e-N曲线，也就是应变幅值-寿命曲线，通过向试件施加不同幅值的正弦载荷，获取整条e-N曲线：

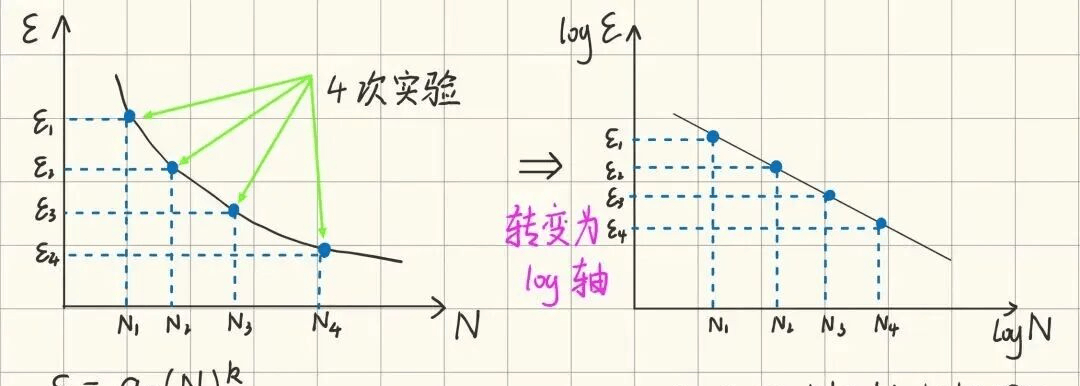
由图中可观察得出，载荷幅值ε 与循环次数寿命N之间的关系表示为图下方的两种表达式。

特别指出的是，图中的纵坐标不一定只是载荷幅值，还可以是应变能密度（SED），最大主柯西应力（S_max），开裂能密度（CED），最大主应变（E_max），等效拉伸应变（E_equiv）

此处主要还是详细讨论，e-N曲线求解疲劳寿命的方法。

1.2 应变比对寿命预测的影响

我们知道，在实验获取e-N曲线过程中，使用的是不同应变幅值的动载荷，而动载荷最大的特点就是，可以动的参数很多，幅值，频率，应变比等等。而橡胶e-N曲线纵坐标只有应变幅值，其他信息表示不出来，故而我们有必要规定，e-N曲线中不同的点，对应橡胶动载荷的应变比、频率不变，应变幅值改变，如下图所示：

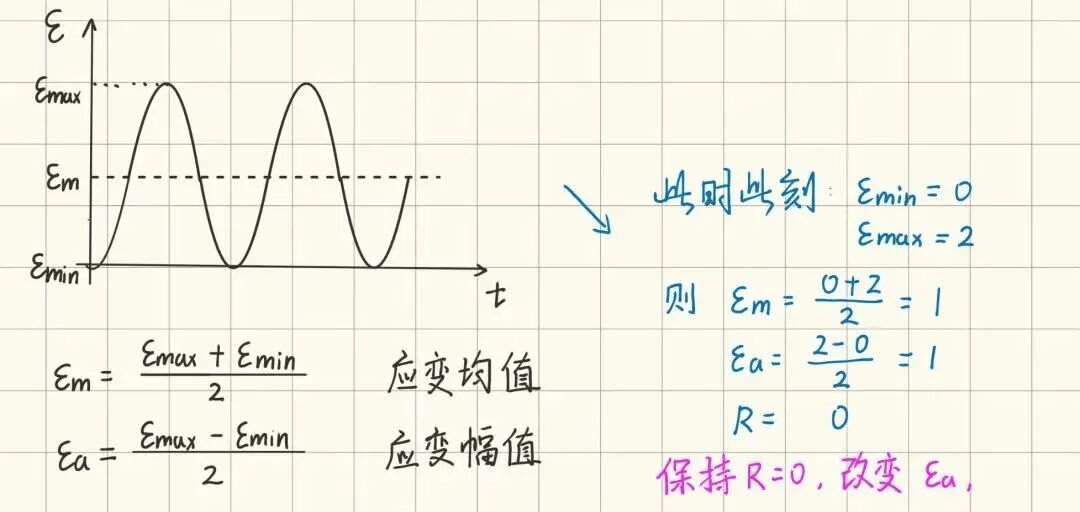
也正因为如此，我们用e-N曲线预测疲劳寿命时候，其实有个隐藏条件，就是应变比是0，比如，应变比是0，应变幅值是2时，寿命是10万次…

问题来了，假如现在，我们只有应变比R为零时候的e-N曲线，却想知道应变比R为0.5，应变幅值是3时候橡胶的寿命，怎么办？

在金属疲劳寿命领域，有典型的Goodman，Soderberg法则来考虑应变比对疲劳寿命的影响，

橡胶与金属有所不同，所以要求出等效应变幅值，通常使用Tao提出的方法：

本质上这些公式是求出一个等效应变幅值，代入e-N曲线中，求解寿命。

在Tao方法中，是把应变比R为其他值的动载荷，等效为应变比为R=-1时候的动载荷。但是，对于填充橡胶结构件，建立应变比R=0的等效应变幅值计算模型更为合适。因为，橡胶的e-N曲线，通常是在R=0动载荷下测试获取的。

故，我们需要对Tao方法，做出改进，如下图所示：

经过以上操作，求出的等效应变幅值，即为应变比R=0时的等效应变幅值。

1.3 累计疲劳损伤准则

如果，橡胶试件承受的动载荷，是变化的，一会幅值是1，一会儿幅值是3，一会儿应变比为0，一会应变比为0.3，等等，如何求解疲劳寿命？

这就引入了累计疲劳损伤准则，Miner准则，即线性疲劳损伤累积准则。

Miner准则对于载荷的加载顺序，载荷的相互作用都不考虑，但是，载荷的加载顺序和载荷的相互作用对疲劳寿命的影响，还挺显著，故而非线性的疲劳损伤累积准则被提出，用来解决这个问题。

此处就不详细解释非线性疲劳损伤累积准则的，总之，这些准则的作用，就是用来解决变幅值载荷下的疲劳寿命的。

1.4 随机载荷下的疲劳寿命

相较于恒幅载荷和变幅载荷工况，随机载荷工况下橡胶隔振器的疲劳损伤机理更为复杂，且更能反映橡胶隔振器的真实疲劳特性。

载荷块编制是实现随机载荷工况下橡胶隔振器疲劳寿命预测的有效手段。载荷块编 制的基本原理是将全寿命周期下的橡胶隔振器载荷谱编制为多级载荷块。

载荷块定义为包含载荷幅值、载荷均值和循环频次的恒幅载荷分量。因此，基于载荷块编制的橡胶隔振器疲劳寿命预测的本质是将随机载荷寿命预测问题转变为恒幅或变幅载荷疲劳寿命预测问题。

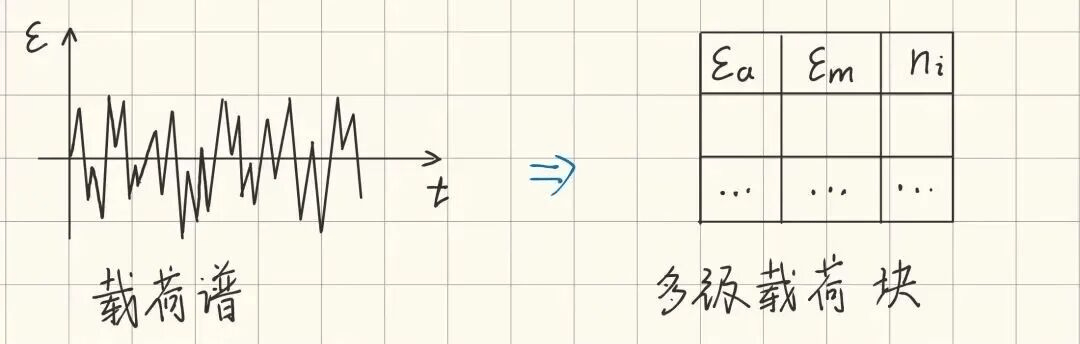
载荷谱统计分析是对载荷谱进行编制的关键步骤之一，现有的载荷谱统计方法主要包括穿级计数、峰谷值计数和雨流计数。

雨流计数作为一种双参数统计方法，可同时统计载荷幅值和载荷均值信息，符合疲劳载荷本身的固有特性。

雨流计数法网上很多专业的讲解，此处就不详细展开了。

随机载荷下疲劳寿命预测思路大抵如此。

2.裂纹扩展法

裂纹扩展法基于断裂力学理论，描述已有裂纹在循环载荷下的增长行为。

裂纹扩展法试件通常设置有初始缺陷：

裂纹扩展法，通常是求解裂纹扩展速率，与基于循环最大撕裂能之间的关系，见下图：

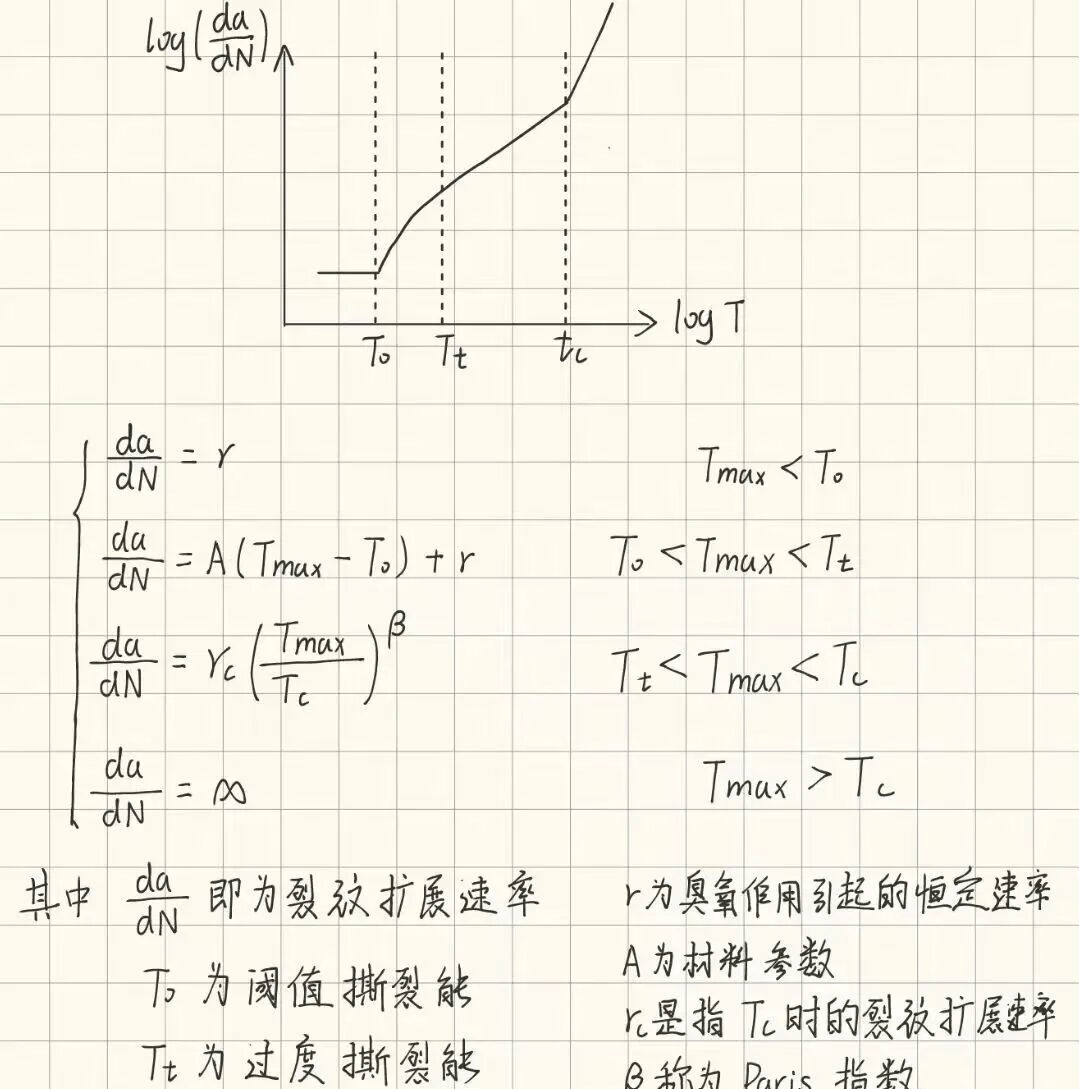
上式实际上表示了裂纹扩展速率与载荷Tmax之间的关系，那现在就存在两个问题：

1.式中的未知参数如T0，Tc等，如何获取？

2.如何根据此式，求解疲劳寿命？

首先解决第一个问题：

裂纹扩展速率与撕裂能之间的关系，即上图中的曲线，可以通过FCGR测试获取。

FCGR测试（Fatigue Crack Growth Rate test，疲劳裂纹扩展速率测试）是评估橡胶材料在循环载荷下裂纹扩展行为的关键实验方法。

所谓的FCGR测试，就是对试件施加不同的应变幅值，进而控制不同大小的撕裂能，观察裂纹的扩展速率，描点，便可获取整条曲线。

理论上说，获取整条曲线之后，公式中的未知参数便可直接拟合获取。

但是获取整条曲线，需要很多很多次实验，非常麻烦，故可以使用一些其它招式获取。

T0为阈值撕裂能，小于该值，寿命无限，可以使用Lake-Yeoh切割法，结合内在强度分析仪（ISA）进行测量。

内在强度分析仪（ISA），其主体结构如图所示。该仪器能精确控制切割速率和应变，确保测量的一致性。

在室温下，对复合材料样品施加几个应变水平，如2%，4%，8%，10%等，每个应变水平，代表不同的初始撕裂能。

每个应变水平下，以不同的切割速率进行切割，如，10 mm/min、0.1 mm/min、0.01 mm/min。

切割时记录切割力f，计算切割能F=f/t（t为样品厚度）；

同步记录撕裂能T（通过应力-应变曲线积分得到）；

仪器自动记录每个切割点的T和F，绘制T与F的关系曲线；

记录曲线与F轴的截距为S0；

代入公式T0=b*S0，求得T0。

Lake-Thomas方程，可以计算T0的理论值，可以与实验结果对比，观察是否一致

临界撕裂能Tc的获取办法，简单很多，对试件施加准静态拉伸，寻找应力应变曲线中，应力随应变增加而下降的第一个点。

过度撕裂能Tt，为曲线中线性区转向幂律如的转折点，通过FCGR测试与Lake-Lindley模型拟合获得。

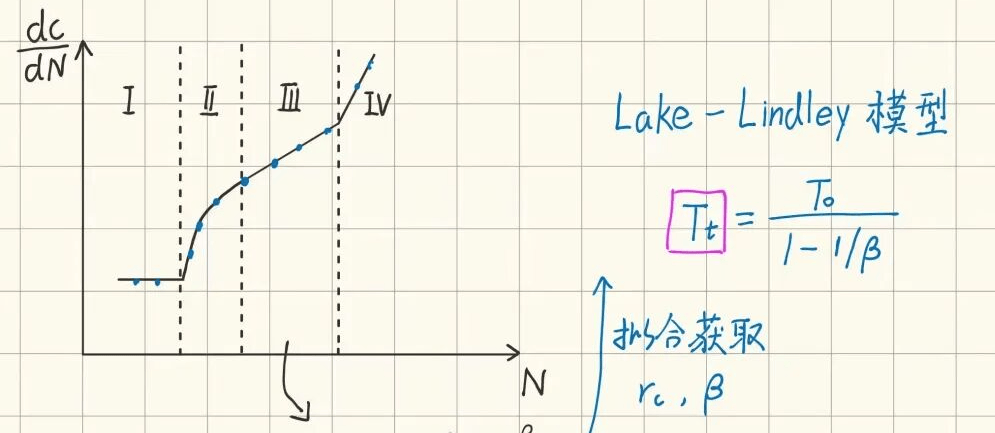
总之，使用FCGR测试，可以获取完整的曲线，使用一些方法，如内在强度分析仪（ISA），可以获得T0……等等。

针对第二个问题：如何根据这条曲线，求解疲劳寿命？

在疲劳裂纹扩展理论中，整合预先存在的缺陷的扩展速率获得的，如从其初始尺寸 a0 到临界尺寸 af所用的循环次数。最准确的疲劳寿命预测是在四种状态下进行分段积分。捷径是在缺陷的整个生命周期内假设幂律行为，即III阶段。

集成过程详见下图：

到此，裂纹扩展法求解疲劳寿命，基本介绍完毕。

3.总结

橡胶疲劳寿命研究的裂纹形核法与裂纹扩展法在理论深度和应用广度上持续拓展。裂纹形核法通过微观损伤累积机制揭示疲劳起源，但需解决多轴统计与配方普适性挑战；裂纹扩展法依托断裂力学实现高精度预测，模型正从经验公式向物理信息AI融合演进。实验技术的革新，特别是多轴高频测试与原位表征，为模型验证提供新维度。未来研究需聚焦跨尺度机理贯通、机器-物理模型深度融合以及全寿命预测框架构建，以满足高性能橡胶构件在工况下的可靠性需求。两种方法的协同应用将推动橡胶疲劳研究进入智能化、精准化的新阶段。